Prolog Übung
zur Vorlesung Logik in der Informatik
Aktuelles
-
Beachten Sie: Für die Nutzung der Rechner der RBG in der Übung, wie auch für den Zugang des Referenzrechners, ist zwingend (seit diesem Semester) ein Informatik-Account notwendig (hier rechtzeitig beantragen). Ein Zugang mittels CMS-Account ist nicht mehr möglich.
- Die Prolog-Übung findet erstmalig in der zweiten Woche der Vorlesungszeit statt, also am 22.10.24.
Abgabehinweise
Abgabehinweise für die -digitale- Abgabe der Prolog-Übungsaufgaben über moodle (ab Übungsblatt 3).
Die Abgabe der Datei mit dem Prolog-Quellcode muss den Namen blattx.pl tragen, wobei x durch die aktuelle Blattnummer ersetzt wird. So sollte die Datei für die Abgabe von Aufgabe 4 von Blatt 3 den Namen blatt3.pl tragen.
In jeder Abgabe soll das Prädikat matnr/1 exakt für Ihre Matrikelnummer gelten. Wenn Sie also die Matrikelnummer 123456 haben, soll Prolog auf die Anfrage ?- matnr(X). mit X = 123456. antworten. Wird die Datei über einen moodle-Account abgegeben, werden frühere Abgaben für diese Aufgabe überschrieben.
Beachten Sie, dass wir Ihre Bearbeitung dieser Aufgaben nur dann bewerten, wenn sich der abgegebene Prolog-Quellcode von SWI-Prolog auf gruenau6 ohne Fehlermeldungen laden lässt und die Abarbeitung gegebener Beispielanfragen nicht länger als 10 Sekunden dauert!
Korrekturanmerkungen zu Ihren Prolog-Abgaben können in Moodle unter Bewertungen (in der Navigationsleiste) eingesehen werden.
Downloads
Hier finden Sie zu gegebener Zeit die für die Lösung einzelner Aufgaben benötigten Dateien:
- Die in Aufgabenblatt 1 beschriebene Wissensbasis b1a4.pl
Beispiele aus der Übung
Definition eines Suchbaumes:
Ein Suchbaum der Anfrage A über der Wissensbasis WB ist eine Erweiterung eines geordneten Baums dessen Knoten und Kanten Beschriftungen tragen können mit den folgenden Eigenschaften:
- Die Wurzel ist mit A gekennzeichnet.
- Alle Knoten sind mit einer Anfrage beschriftet, insbesondere enthalten Blätter entweder die leere Anfrage oder sind zusätzlich unterhalb der Blätter mit † gekennzeichnet.
- Ein Blatt ist genau dann zusätzlich mit † gekennzeichnet, falls der erste Term der Anfrage (Beschriftung des Blattes) mit keinem Kopf irgendeiner Regel (bzw. Fakt) aus WB unifiziert werden kann.
- Ist Knoten v ein Kindknoten von Knoten w, dann
- ) existiert eine Regel r in WB, so dass der erste Term der Anfrage (Beschriftung von w) sich mit dem Kopf von r unifizieren läßt.
- ) Sei r' eine Regel, entstanden aus r, bei der alle Variablen so umbenannt sind, dass sie nicht in der Anfrage vorkommen.
- ) Sei S die Menge der Variableninstanziierungen bei der Unifikation des Kopfes von r' mit dem ersten Term der Anfrage (von w).
- ) Die Beschriftung von v entsteht durch Ersetzen des ersten Terms der Anfrage von w durch den Körper der umbenannten Regel r' und der Ersetzung von Variablen entsprechend S.
- ) Die Instanziierungen der Variablen des ersetzten Terms der Anfrage stehen an der Kante von w nach v.
- Knoten v mit Beschriftung A besitzt für jede Regel r, deren Kopf sich mit dem ersten Term der Anfrage A unifizieren läßt, einen Kindknoten. Die Reihenfolge der Kindknoten, wird durch die Reihenfolge der Vorkommen der angewendeten Regeln in WB bestimmt.
Woche 01
geld_verbrannt.
lachgas.
woman(jody).
woman(yolanda).
loves(vincent, mia).
loves(marsellus, mia).
playsAirGuitar(jody).
party.
loves(ramona,todd).
time_flies(_).
ramonasEvilExes(lucas).
ramonasEvilExes(X) :- time_flies(X), loves(ramona,X).
fights(knives,X):-loves(X,scott).
fights(scott,X):- ramonasEvilExes(X).
loves(ramona,roxy).
loves(ramona,todd).
time_flies(_).
ramonasEvilExes(lucas).
ramonasEvilExes(X) :- time_flies(X), loves(ramona,X).
fights(knives,X):-loves(X,scott).
fights(scott,X):- ramonasEvilExes(X).
Woche 02
loves(mia,X) :- good_dancer(X).
kills(marsellus,X) :- loves(mia,X).
f(b).
g(a).
g(b).
h(b).
k(X) :- f(X), g(X), h(X).
Programmieren mit Unifikation:
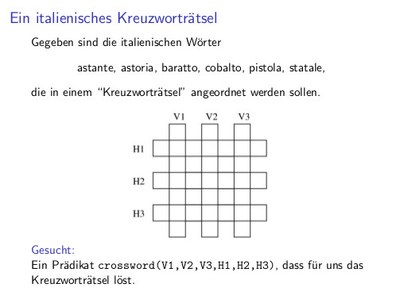
Aufgabe 2.4 aus [BBS]
Die Worte werden dabei wie folgt in der Wissensbasis repräsentiert:
word(astoria, a,s,t,o,r,i,a).
word(baratto, b,a,r,a,t,t,o).
word(cobalto, c,o,b,a,l,t,o).
word(pistola, p,i,s,t,o,l,a).
word(statale, s,t,a,t,a,l,e).
Programmieren mit Nicht-Unifizierbarkeit:
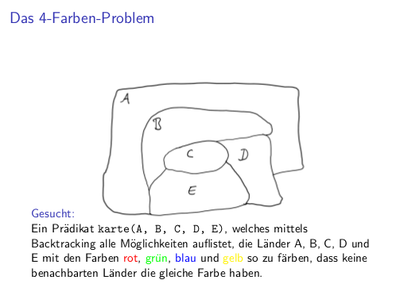
Woche 03
kind(brigitte, carolin).
kind(carolin, donna).
kind(donna, emilie).
nachkomme(X, Y) :- kind(X, Y).
nachkomme(X, Y) :- kind(X, Z), nachkomme(Z, Y).
kind(brigitte, carolin).
kind(carolin, donna).
kind(donna, emilie).
nachkomme(X, Y) :- kind(X, Z), nachkomme(Z, Y).
nachkomme(X, Y) :- kind(X, Y).
kind(brigitte, carolin).
kind(carolin, donna).
kind(donna, emilie).
nachkomme(X, Y) :- nachkomme(Z, Y), kind(X, Z).
nachkomme(X, Y) :- kind(X, Y).
kind(brigitte, carolin).
kind(carolin, donna).
kind(donna, emilie).
nachkomme(X, Y) :- kind(X, Y).
nachkomme(X, Y) :- nachkomme(Z, Y), kind(X, Z).
numeral(succ(X)) :- numeral(X).
double(succ(X),succ(succ(Y))) :- double(X,Y).
add(0,Y,Y).
add(succ(X),Y,succ(Z)):- add(X,Y,Z).
greater(succ(_),0).
greater(succ(X),succ(Y)):-greater(X,Y).
offen:
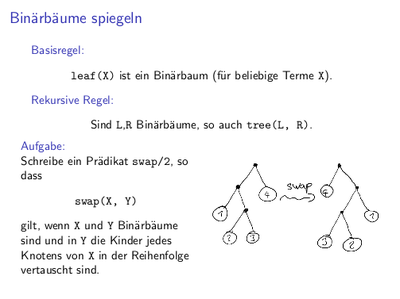
Woche 04
element(X,[_|T]) :- element(X,T).
invert([a|T1],[b|T2]) :- invert(T1,T2).
invert([b|T1],[a|T2]) :- invert(T1,T2).
evenElements([], []).
evenElements([_, X|T1], [X|T2]) :- evenElements(T1,T2).
Woche 05
laenge([_|T],L) :- laenge(T,LT),L is LT + 1.
laenge([_|T],A,N) :- AT is A + 1 , laenge(T,AT,N).
laenge(L, N) :- laenge(L,0,N).
prod([], A, A).
prod([H|T], A, P) :- A2 is A * H, prod(T, A2, P).
max([H|T], A, MT) :- H > A, max(T, H, MT).
max([H|T], A, MT) :- H =< A, max(T, A, MT).
max([H|T], M) :- max(T, H, M).
% CAKE
% STORY
ziffer(0).
ziffer(1).
ziffer(2). ziffer(3). ziffer(4). ziffer(5).
ziffer(6). ziffer(7). ziffer(8). ziffer(9).
raetsel(F, A, K, E, C , S, T, O, R,Y) :-
ziffer(F), ziffer(A), ziffer(K), ziffer(E),ziffer(C),
ziffer(S), ziffer(T), ziffer(O), ziffer(R), ziffer(Y),
F =\= A, F =\= K , F =\= E, F =\= C, F =\= S, F =\= T, F =\= O, F =\= R, F =\= Y,
A =\= K , A =\=E, A =\=C, A =\=S, A =\=T, A =\=O, A =\=R, A =\=Y,
K =\=E, K =\=C, K =\=S, K =\=T, K =\=O, K =\=R, K =\=Y,
E =\=C, E =\=S, E =\=T, E =\=O, E =\=R, E =\=Y,
C =\=S, C =\=T, C =\=O, C =\=R, C =\=Y,
S =\=T, S =\=O, S =\=R, S =\=Y,
T =\=O, T =\=R, T =\=Y,
O =\=R, O =\=Y,
R =\=Y,
S =\= 0, C =\= 0, F =\= 0,
Y =:= (E + E) mod 10, U1 is (E + E) // 10,
R =:= (K + K + U1) mod 10, U2 is (K + K + U1) // 10,
O =:= (A + A + U2) mod 10, U3 is (A + A + U2) // 10,
T =:= (F + C + U3) mod 10, S =:= (F + C + U3) // 10.
% Try:
% ?- time(findall([F, A, K, E, C , S, T, O, R,Y],raetsel(F, A, K, E, C , S, T, O, R,Y),Z)).
% CAKE
% STORY
ziffer(0).
ziffer(1).
ziffer(2). ziffer(3). ziffer(4). ziffer(5).
ziffer(6). ziffer(7). ziffer(8). ziffer(9).
raetsel(F, A, K, E, C , S, T, O, R,Y) :-
ziffer(E),
Y is (E + E) mod 10, U1 is (E + E) // 10,
ziffer(K),
R is (K + K + U1) mod 10, U2 is (K + K + U1) // 10,
ziffer(A),
O is (A + A + U2) mod 10, U3 is (A + A + U2) // 10,
ziffer(F), ziffer(C),
T is (F + C + U3) mod 10, S is (F + C + U3) // 10,
F =\= A, F =\= K , F =\=E, F =\=C, F =\=S, F =\=T, F =\=O, F =\=R, F =\=Y,
A =\= K , A =\=E, A =\=C, A =\=S, A =\=T, A =\=O, A =\=R, A =\=Y,
K =\=E, K =\=C, K =\=S, K =\=T, K =\=O, K =\=R, K =\=Y,
E =\=C, E =\=S, E =\=T, E =\=O, E =\=R, E =\=Y,
C =\=S, C =\=T, C =\=O, C =\=R, C =\=Y,
S =\=T, S =\=O, S =\=R, S =\=Y,
T =\=O, T =\=R, T =\=Y,
O =\=R, O =\=Y,
R =\=Y,
S =\= 0, C =\= 0, F =\= 0.
% Try:
% ?- time(findall([F, A, K, E, C , S, T, O, R,Y],raetsel(F, A, K, E, C , S, T, O, R,Y),Z)).
Offen: Der Klassiker der Rekursion
Die Fakultät n! einer natürlichen Zahl n ist definiert durch:
Definieren Sie
- ein Prädikat fak/2, dass bei Anfrage fak(X,Y) die Fakultät von X mit Y unifiziert.
- ein Prädikat fakAcc/2, dass äquivalent zu fak/2 ist und "End-Rekursiv” realisiert.
Literatur
| [BBS] | Patrick Blackburn, Johan Bos, Kristina Striegnitz, Learn PROLOG Now!. Kings College Publications, 2006. Online version. |
| [SS] | Ehud Shapiro, Leon Sterling, The Art of PROLOG: Advanced Programming Techniques. 2nd Edition, MIT Press, 1994. |
Programmierressourcen
SWI-Prolog. Eine Kurzanleitung für den Einstieg in SWI-Prolog.